Latest earthquakes near Lyon, Auvergne-Rhône-Alpes today
Complete overview of the latest earthquakes near Lyon, Auvergne-Rhône-Alpes, France, updated every minute. Did you feel an earthquake today in Lyon? If an earthquake is happening right now near Lyon, it will show up within minutes.
Lyon Earthquake Statistics
Average
A total of 19 earthquakes with a magnitude of four or above have struck within 300 km (186 mi) of Lyon, Auvergne-Rhône-Alpes in the past 10 years. This comes down to a yearly average of 1 earthquakes per year
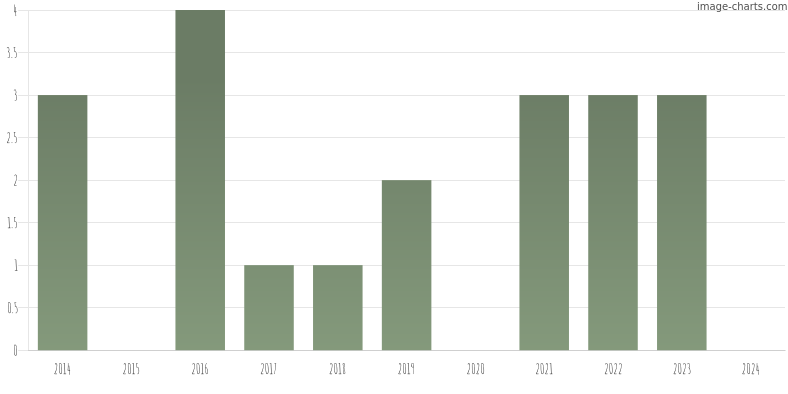
Magnitude Distribution
The table below visualizes the distribution of all earthquakes that occurred within 300km of Lyon in the past 10 years. No earthquakes with a magnitude of 5 or above have occurred near Lyon during this time. Usually, higher magnitudes are less common than lower magnitudes. Small earthquakes with a magnitude below 4 on the Richter scale have been omitted from this overview.
| Magnitude | Earthquakes | Percentage |
|---|---|---|
| Mag. 4 | 19 | 100.0% |
| Mag. 5 | 0 | 0.0% |
| Mag. 6 | 0 | 0.0% |
| Mag. 7 | 0 | 0.0% |
| Mag. 8 | 0 | 0.0% |
| Mag. 9 | 0 | 0.0% |
| Mag. 10 | 0 | 0.0% |
Strongest earthquakes near Lyon
The strongest recent earthquake of the past 10 years near Lyon occurred on Nov 11, 2019 11:52 local time (Europe/Paris timezone). It had a magnitude of 4.8 and struck 127 kilometers (79 mi) south of Lyon, at a depth of 10 km. Discover more strong earthquakes near Lyon in the list below.
A longer time ago, a MAG-6.2 earthquake struck on Jan 25, 1946 18:31, 231 kilometers (144 mi) south of Lyon. It is the strongest earthquake near Lyon in the past 124 years (Our data goes back to January 1st, 1900).
In the table below you will find the strongest earthquakes that occurred near Lyon, Auvergne-Rhône-Alpes in the past 10 years. You can use the tabs to find the heaviest historic earthquakes since the year 1900 or within a specific year or distance from Lyon.
Nearest earthquakes from Lyon
These are the earthquakes with their epicenter nearest to Lyon, Auvergne-Rhône-Alpes. You can use the buttons to find nearby earthquakes for a specific year or with a specific magnitude.
Frequently Asked Questions
These questions are commonly asked in relation to earthquakes occurring near Lyon.
When was the last earthquake in Lyon, Auvergne-Rhône-Alpes?
A 2.1 magnitude earthquake hit near Lyon on the evening of April 27, 2024 at 20:28 local time (Europe/Paris). The center of this earthquake was located 211km east-southeast of Lyon at a depth of 5km under land. Check the list on our website for any earthquakes occurring near Lyon, Auvergne-Rhône-Alpes in the past hours.
What was the strongest earthquake near Lyon, Auvergne-Rhône-Alpes?
A 6.2 magnitude earthquake hit near Lyon on the evening of January 25, 1946 at 18:31 local time (Europe/Paris). The center of this earthquake was located 231km east-northeast of Lyon at a depth of 10km under land. This is the strongest earthquake that occurred near Lyon since the year 1900.
How often do earthquakes occur near Lyon, Auvergne-Rhône-Alpes?
In the past 10 years, 19 earthquakes with a magnitude of four or higher occurred within a 300 kilometer range from Lyon. This averages to 2 earthquakes yearly, or one earthquake every 192 days.

